This article represents Part 2 of a two-part series giving the basics of measurement uncertainty. Part 1 covered the concepts, definitions and nomenclature of measurement uncertainty whilst this article gives a worked example of measurement uncertainty based around the measurement of the volume of a cylindrical oil tank.
The cost of uncertainty
In all measurement systems, it is generally the case that the lower the required measurement uncertainty, the higher the financial cost required to achieve it (see Figure 1). Thorough evaluation of the system uncertainty helps ensure that the metering system is properly designed, cost-effective and fit for purpose, meeting any uncertainty constraints specified legally, through partner agreements or through internal requirements.
Uncertainty analysis is an essential component of the design and use of any measurement system. Without a thorough uncertainty analysis, time and money will be wasted on inappropriate instrumentation. As discussed, the techniques used for performing the analysis are not complicated but must be based on the solid foundation of a detailed review of the entire measurement process.
Example 1: The cost of uncertainty
Suppose you are filling your car with petrol, the uncertainty in the flow of fuel is 2 % at the 95 % confidence level. If the capacity of your fuel tank is 70 litres, what is the uncertainty of half filling the tank? The volume of flow is given by:
35.0 ± 0.7 litre at 95% confidence
If the cost of petrol is £1.50 per litre, what is the cost of half filling the tank?
£52.50 ± £1.05 at 95 % confidence
The Standard (GUM) method of Uncertainty
For a more detailed explanation of all the steps and calculations required to undertake an uncertainty calculation, the reader is asked to consult the ISO/IEC “Guide to the expression of uncertainty in measurement (GUM)”. The following example shows a simple case of how the uncertainty of a measurement can be developed.
To undertake a measurement uncertainty calculation a few rules must be followed:
- Can only add like to like
- Keep to absolute (or relative) uncertainties
- Can only add uncertainties at a common confidence level
- Therefore we must reduce all uncertainties to standard uncertainties
- Can only add in common units
- Cannot add kg and °C
- Express everything in terms of contribution to final uncertainty (i.e. m3 in our example)
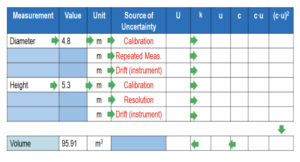
Table 1 shows how the uncertainty budget calculation should be determined. The individual sources of uncertainty are calculated horizontally along the rows of the table. this allows all sources of uncertainty to be at a standard level of uncertainty (u). The overall uncertainty is then calculated by adding the values of (c.u)2 vertically down the table and then calculating each of the values listed in the table by following the arrows shown in Table 1. This allows the overall uncertainty of the measurement to be calculated.
Table 1: Volume of a Cylindrical Tank
Where:
U Expanded Uncertainty (usually quoted at 95% confidence limits)
k Coverage Factor (for 95% Confidence levels this equals 1.96)
u Standard Uncertainty (68% Confidence level)
c Sensitivity Co-efficient
Where the sensitivity co-efficient represents how the variables in an equation or function are related to the calculated result. When a small change is made in the variable x in an equation it will have an effect on the magnitude of the result y. So, in the example, by making small changes in both the height and diameter, it is possible to determine the sensitivity of the variable (height or diameter) to the overall result (volume).
Example 2: Uncertainty of a tank volume
We require to calculate the uncertainty in the volume of a cylindrical oil tank. The height of the tank is nominally 5.3 m, and its diameter is 4.8 m.
Where volume is calculated using:
V=d2h4
To do this we must measure both the height and diameter of the vessel. The sources of uncertainty are therefore those in the measurement of height and diameter.
The value of the volume calculated using the above equation and the values measured above is 95.91 m3. It is now possible to determine the uncertainty of this measurement using the following procedure.
Height measurement
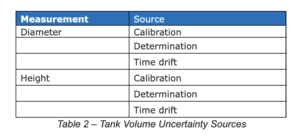
The principal sources of uncertainty in this measurement are the calibration of the measuring instrument, its resolution, and any changes in the height due to time drift.
Diameter measurement
The uncertainty sources in the diameter are similar to those in the height measurement. The uncertainty in the instrument calibration and temporal variation in the diameter are both important. The tank may not always be a perfect cylinder, so the diameter may vary depending on which part of the circumference the measurement is made. The resolution of the measuring instrument is also an important source. In this case, for convenience, the final three sources are combined into a single source, the standard uncertainty is determined directly.
Tank volume uncertainties
Summarizing the information contained above the principal tank volume uncertainty sources are shown in Table 2.
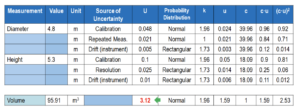
Overall tank volume uncertainty budget
Table 3 lists all the sources of uncertainty in the diameter, height, and volume variation measurements and gives you the uncertainty of the volume measurement of the storage tank, in this case the uncertainty is:
95.91 ± 3.12 m3 at 95% confidence
The importance of uncertainty in measurement
Table 3 – Overall Tank Volume Uncertainty Budget
This example shows a very simplified case of a measurement uncertainty calculation. If you are interested in learning more concerning the use of uncertainty budgets and how they are calculated, TÜV SÜD National Engineering Laboratory offer training courses on measurement uncertainty. If you wish to discuss any issues regarding measurement uncertainty and the development of uncertainty budgets, we would be happy to discuss any issues you may be having.